One of the new additions in 4.67.x/4.68.x BETA
is portfolio backtester programming interface providing full control of 2nd
phase of portfolio backtest. This allows multitude of applications including, but not limited to:
Technical reference of new interface is available here, in this chapter we will just focus on some practical examples.
Adding user-defined metrics
Example 1
Let's start with the easiest application: in the very first example I will show you how to add user-defined metric to portfolio report and optimization result list.
In the first step we will add Expectancy to backtest and optimization report. There is some discussion about how expectancy should be calculated but the easiest formula for it is:
Expectancy ($) = %Winners * AvgProfit - %Losers * AvgLoss
or (the other way of calculating the same)
Expectancy ($) = (TotalProfit - TotalLoss) / NumberOfTrades = NetProfit / NumberOfTrades
Let us start with this simple formulation. With this approach expectancy simply tells us expected profit per trade in dollars. The custom backtest formula that implements this user-defined metric looks as follows:
/*
First we need to enable custom backtest procedure and
** tell AmiBroker to use current formula
*/
SetCustomBacktestProc("");
/* Now custom-backtest procedure follows */
if( Status("action")
== actionPortfolio )
{
bo = GetBacktesterObject();
bo.Backtest(); // run default backtest procedure
st = bo.GetPerformanceStats(0); //
get stats for all trades
// Expectancy calculation (the
easy way)
// %Win * AvgProfit - %Los *
AvgLos
// note that because AvgLos is
already negative
// in AmiBroker so we are adding
values instead of subtracting them
// we could also use simpler formula
NetProfit/NumberOfTrades
// but for the purpose of
illustration we are using more complex one :-)
expectancy = st.GetValue("WinnersAvgProfit")*st.GetValue("WinnersPercent")/100 +
st.GetValue("LosersAvgLoss")*st.GetValue("LosersPercent")/100;
// Here we add custom metric to
backtest report
bo.AddCustomMetric( "Expectancy ($)",
expectancy );
}
// your trading system here
fast = Optimize("fast", 12, 5, 20, 1 );
slow = Optimize("slow", 26, 10, 25, 1 );
Buy=Cross(MACD(fast,slow),Signal(fast,slow));
Sell=Cross(Signal(fast,slow),MACD(fast,slow));
First we need to tell AmiBroker to use custom backtest formula instead of built-in one. We are doing so by calling SetCustomBacktestProc. First parameter defines the path to the custom backtest formula (which can be stored in some external file, independent from actual trading system). If we provide empty string there, we are telling AmiBroker to use current formula (the same which is used for trading system).
In the next line we have "if" statement that enters custom backtest formula if the analysis engine is in actionPortfolio (2nd phase of portfolio backtest) stage. This is important as formula is executed in both scanning phase (when trading signals are generated) and in actual portfolio backtest phase. "if" statement allows us to enter custom backtest procedure part only when analysis engine is in actual backtesting phase.
In the next line we obtain the access to backtester programming interface by calling GetBacktesterObject function. This returns Backtester object that is used to access all functionality of new interface (more details on objects available see: http://www.amibroker.com/docs/ab401.html)
Later we obtain access to built-in metrics by calling GetPerformanceStats method of backtester object. This method returns Statistics object that allows us to access any built-in metric by calling GetValue method.
As a next step we calculate expectancy value from built-in metrics retrieved using GetValue method. For the list of metrics supported by GetValue method please check: http://www.amibroker.com/docs/ab401.html
In the final step we simply add our custom metric to the report by calling AddCustomMetric function of Backtester object. The first parameter is the name of the metric, the second is the value.
After "if"-statement implementing our custom backtest procedure usual trading system rules follow.
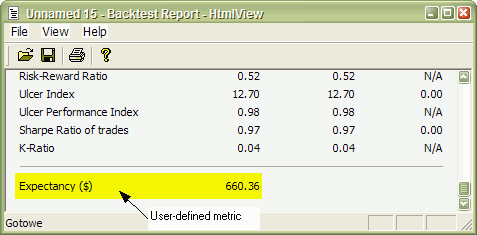
Now when you run Backtest and click Report button in Automatic Analysis window you will see your custom metric added at the bottom of statistics page:

User-defined metric also appears in the Optimization result list:
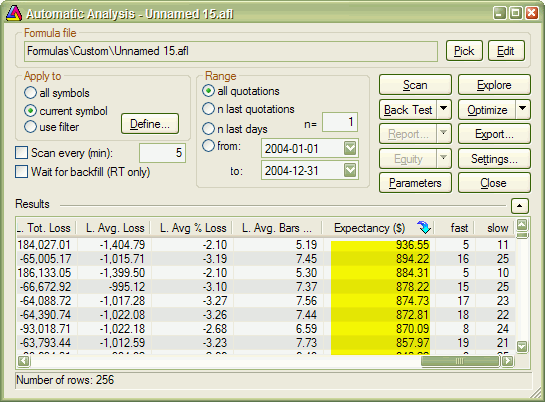
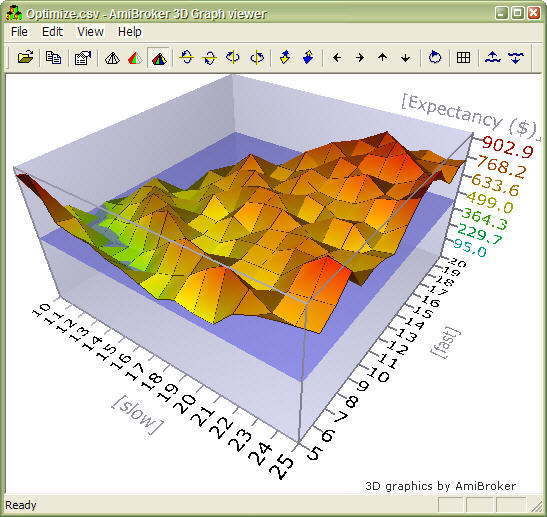
When you click on the custom metric column, the optimization results will be sorted by your own metric and you will be able to display 3D chart of your user-defined metric plotted against optimization variables.
Example 2
Some people point out that this simple method of calculating expectancy works well only with constant position size. Otherwise, with variable position sizing and/or compounding, larger trades weight more than smaller trades and this leads to misleading expectancy values. To address this problem one could calculate expectancy for example as expected profit per $100 invested. To do calculate such statistic, one needs to iterate through trades, summing up profits per $100 unit, and dividing this sum by the number of trades. Appropriate formula follows:
/* First we need to enable
custom backtest procedure and
** tell AmiBroker to use current formula
*/
SetCustomBacktestProc("");
/* Now custom-backtest procedure follows */
if( Status("action")
== actionPortfolio )
{
bo = GetBacktesterObject();
bo.Backtest(); // run default backtest procedure
SumProfitPer100Inv = 0;
NumTrades = 0;
// iterate through closed trades
first
for(
trade = bo.GetFirstTrade(); trade; trade = bo.GetNextTrade() )
{
// here we sum
up profit per $100 invested
SumProfitPer100Inv = SumProfitPer100Inv + trade.GetPercentProfit();
NumTrades++;
}
// iterate through eventually still open positions
for(
trade = bo.GetFirstOpenPos(); trade; trade = bo.GetNextOpenPos() )
{
SumProfitPer100Inv = SumProfitPer100Inv + trade.GetPercentProfit();
NumTrades++;
}
expectancy2 = SumProfitPer100Inv / NumTrades;
bo.AddCustomMetric( "Expectancy (per $100 inv.)",
expectancy2 );
}
// your trading system here
fast = Optimize("fast", 12, 5, 20, 1 );
slow = Optimize("slow", 26, 10, 25, 1 );
Buy=Cross(MACD(fast,slow),Signal(fast,slow));
Sell=Cross(Signal(fast,slow),MACD(fast,slow));
The only difference between this and previous formula is that we do not use built-in metrics to calculate our own expectancy figure. Instead we sum up all percentage profits of each trade (which are equivalent to dollar profits from $100 unit investment) and at the end divide the sum by the number of trades. Summing up is done inside the "for" loop. GetFirstTrade/GetNextTrade function pair of the backtester object allows us to step through the list of closed trades. We use two loops (second loop uses GetFirstOpenPos/GetNexOpenPos) because there may be some open positions left at the end of the backtest. If we wanted to include only closed trades then we could remove second "for" loop.
After running this code we find out that expectancy calculated this way even adjusted to initial equity (by multiplying by factor InitialEquity/$100) is smaller than expectancy calculated in the first example. This shows that "easy" method of expectancy calculation (from example 1) may lead to overly optimistic results.
Example 3
Some Van Tharp followers prefer yet slightly differnt "twist" of expectancy measure. They express expectancy in terms of expected profit per "unit of risk". The profit is then expressed in terms of R-multiples, where 1R is defined as the amount risked per trade. The amount risked is the maximum amount of money you can lose, and most often it is set by the amount of maximum loss stop (or trailing stop). According to Tharp, the easiest way to calculate expectancy is simply to add up all your R-multiples and net them out by subtracting the negative R-multiples from the positive ones, then divide by the no. of trades. This gives you your expectancy per trade.
This is very similar to approach presented in example 2, but for the calculations we do not use the value of the trade but rather risk per trade. The risk depends on the stop we use in our trading system. For simplicity in this example we have used 10% max. loss stop. In this example we also add per-trade metrics for better illustration of how R-multiples are calculated. Per-trade metrics appear in each row of the trade list in the backtest results.
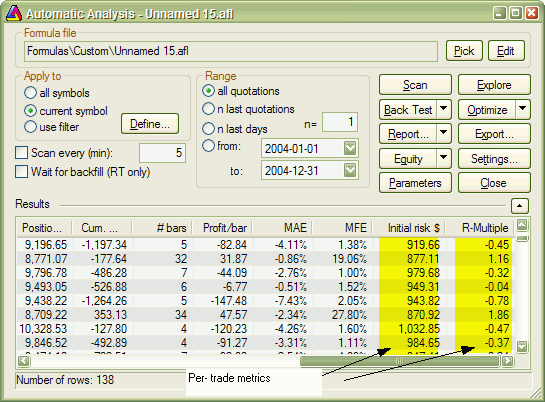
The formula that implements this kind of expectancy measure follows:
/*
First we need to enable custom backtest procedure and
** tell AmiBroker to use current formula
*/
SetCustomBacktestProc("");
MaxLossPercentStop = 10; //
10% max. loss stop
/* Now custom-backtest procedure follows */
if( Status("action")
== actionPortfolio )
{
bo = GetBacktesterObject();
bo.Backtest(1); //
run default backtest procedure
SumProfitPerRisk = 0;
NumTrades = 0;
// iterate through closed trades
first
for(
trade = bo.GetFirstTrade(); trade; trade = bo.GetNextTrade() )
{
// risk is calculated
as the maximum value we can loose per trade
// in this example
we are using max. loss stop
// it means
we can not lose more than (MaxLoss%) of invested amount
// hence ris
Risk = ( MaxLossPercentStop / 100 )
* trade.GetEntryValue();
RMultiple = trade.GetProfit()/Risk;
trade.AddCustomMetric("Initial risk $",
Risk );
trade.AddCustomMetric("R-Multiple",
RMultiple );
SumProfitPerRisk = SumProfitPerRisk + RMultiple;
NumTrades++;
}
expectancy3 = SumProfitPerRisk / NumTrades;
bo.AddCustomMetric( "Expectancy (per risk)",
expectancy3 );
bo.ListTrades();
}
// your trading system here
ApplyStop( stopTypeLoss, stopModePercent,
MaxLossPercentStop );
fast = Optimize("fast", 12, 5, 20, 1 );
slow = Optimize("slow", 26, 10, 25, 1 );
Buy=Cross(MACD(fast,slow),Signal(fast,slow));
Sell=Cross(Signal(fast,slow),MACD(fast,slow));
The code is basically very similar to example 2. There are only few differences. First is that we call Backtest method with NoTradeList parameter set to 1. This way we disable default trade listing, so we can add custom per-trade metrics and list trades later by calling ListTrades method. Later we iterate through trades and calculate risk based on trade entry value and amount of max. loss stop used. The RMultiple is then calculated as trade profit divided by the amount risked per trade. Both risk and r-multiple are then added as custom per-trade metrics (note that we are callind AddCustomMetric method of Trade object here). Later on we do remaining calculations. At the end of the custom backtest procedure we are adding custom backtest metric (this time calling AddCustomMetric method of Backtester object), and after that we trigger listing of the trades using ListTrades method. For simplicity we ignore any open positions that may have left at the end of analysis period. The only change to the trading system itself was addition of maximum loss stop (ApplyStop line).
Conclusion
A new portfolio backtester programming interface provides ability to add user-defined statistics of any kind, allowing the user to move the analysis of backtesting results to completely new level.